Ziehen einer Wurzel - Papier Bleistift Methode
| Herleitung des Verfahrens |
Auf dieser Seite will ich einen Weg vorstellen, eine Quadratwurzel mit Hilfe einer "Papier-Bleistift-Methode" zu ziehen. Wenn man gerade keinen Taschenrechner zur Hand hat, kann einem diese Methode relativ schnell weiterhelfen.
Sie stammt von meinem Mathematikprofessor, nachdem ich zuvor vergebens in Büchern, Zeitschriften und im Internet nach einer befriedigenden Lösung gesucht hatte.
Die Methode anhand eines Beispiels... |
|
| Beschreibung | Beispiel (Quadratwurzel aus 54321) |
|
1. Schritt: Zunächst teilt man die Zahl von rechts beginnend in 2er-Gruppen auf. Dies kann gedanklich oder besser mit kleinen Strichen wie gezeigt erfolgen. |
|
|
2. Schritt: Nun zieht man von der am weitesten links stehende 2er-Gruppe mit 1 beginnend ungerade Zahlen ab. Das macht man solange, wie noch ungerade Zahlen subtrahiert werden können, ohne das der Rest negativ wird. Im Beispiel können von der 2er-Gruppe 5 nur 1 und 3 abgezogen werden. Der Rest ist 1. 3. Schritt: Die Anzahl der ungeraden Zahlen schreibt man dann als erste Ziffer des Ergebnisses hinter dem Gleichheitszeichen. Im Beispiel ist die erste Ergebnis-Ziffer 2. |
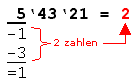 |
|
4. Schritt: Zu dem verbliebenen Rest nimmt man nun die nächste 2er-Gruppe hinzu. Im Beispiel wird zu dem Rest 1 die 2er-Gruppe 43 hinzugefügt. Es entsteht die Zahl 143. 5. Schritt: Das bisherige Ergebnis wird mit 2 multipliziert und um eine Stelle nach links verschoben unter der im Schritt 4 entstandenen Zahl geschrieben. Im Beispiel ist das bisherige Ergebnis 2 multipliziert mit 2 = 4. Die 4 wird um eine Stelle nach links verschoben unter die Zahl 143 geschrieben. |
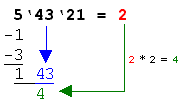 |
|
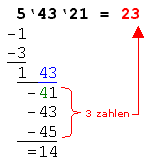
6. Schritt: Die im Schritt 5 entstandene Zahl wird nun im Einer durch 1 erweitert. Mit der so entstandenen Zahl beginnend, zieht man wieder wie im Schritt 2 die ungeraden Zahlen von der im Schritt 4 entstandenen ab. Im Beispiel ergibt sich nach der Erweiterung mit 1 die Zahl 41. Beginnend mit der 41 können nun die Zahlen 41, 43 und 45 von der Zahl 143 abgezogen werden ohne das der Rest negativ wird. Der Rest beträgt nun 14. 7. Schritt: Analog zum Schritt 3 ergibt nun wieder die Anzahl der abgezogen ungeraden Zahlen die nächste Ziffer im Ergebnis. Im Beispiel ist das die Ziffer 3, wodurch das Ergebnis auf 23 erweitert wird. |
 |
|
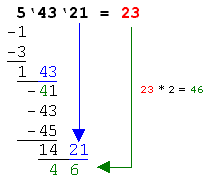
Schritte 4* und 5*: Hier wiederholen sich die Schritte 4 und 5 mit den aktuellen Zahlen. Im Beispiel wird der Rest 14 durch die letzte 2er-Gruppe erweitert (=1421). Das Ergebnis wird nun mit 2 multipliziert was 46 ergibt (2 * 23 = 46). Die Zahl 46 wird nun um 1 nach links versetzt unterhalb von 1421 geschrieben. |
 |
|
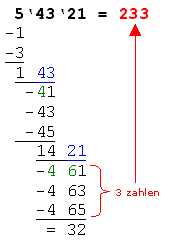
Schritte 6* und 7*: Hier wiederholen sich die Schritte 6 und 7 mit den aktuellen Zahlen. Im Beispiel wird die Zahl 46 im Einer durch 1 ergänzt (=461) und fortfolgend die ungeraden Zahlen 461, 463 und 465 abgezogen. Dadurch ergibt sich ein Rest von 32. Die Anzahl der ungeraden Zahlen (hier 3) ist die nächste Ziffer im Ergebnis, welches nun 233 lautet. |
 |
|
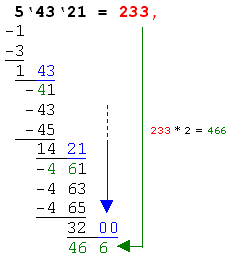
Schritte 4* und 5*: Hier wiederholen sich die Schritte 4 und 5 mit den aktuellen Zahlen. Da keine 2er-Gruppe mehr übrig ist, wird 00 angenommen. Somit beginnen auch die Nachkommastellen im Ergebnis. Im Beispiel wird die Zahl 32 durch 00 ergänzt (=3200). Das Ergebnis wird mit 2 multipliziert (233*2=466) und um 1 nach links verschoben unter 3200 geschrieben. |
 |
|
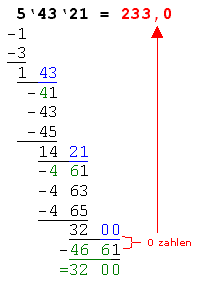
Schritte 6* und 7*: Hier wiederholen sich die Schritte 6 und 7 mit den aktuellen Zahlen. Im Beispiel wird die Zahl 466 um 1 erweitert (=4661). Diese Zahl kann aber nur 0 mal von 3200 abgezogen werden, ohne dass der Rest negativ wird (rest=3200). Somit ergibt sich 0 als nächste Ziffer (Nachkommastelle) im Ergebnis. |
 |
|
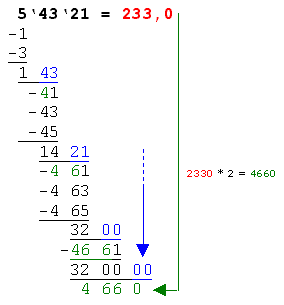
Schritte 4* und 5*: Hier wiederholen sich die Schritte 4 und 5 mit den aktuellen Zahlen. Da keine 2er-Gruppe mehr übrig ist, wird 00 angenommen. Im Beispiel wird der Rest 3200 um die 2er-Gruppe 00 erweitert (=320000). Das Ergebnis wird mit 2 multipliziert (2330*2=4660) und um eine Stelle nach links verschoben unter die Zahl 320000 geschrieben. |
 |
|
Schritte 6* und 7*: Hier wiederholen sich die Schritte 6 und 7 mit den aktuellen Zahlen. Im Beispiel wird die zahl 4660 im Einer um 1 erweitert (=46601). Von 46601 aus beginnend werden nun die ungerade Zahlen abgezogen. Insgesamt sind das 6 Stück wodurch sich das Ergebnis um die Ziffer 6 erweitert. |
 |
|
... Die Schritte 4 bis 7 können solange wiederholt werden, bis das Ergebnis ausreichend genau oder der Rest 0 ist. | |
Weiterführende Seiten... |
|
- Wurzel (Mathematik)
© 2000-2004 Andreas Göbel Impressum · Datenschutz/Cookies
Casio Polynomdivision
Fotos
Kalender Übersicht
Mathematik Übersicht
Impressum - Datenschutz/Cookies
Kalender
P.M. Logiktrainer
Römische Zahlen
Deutsche Schrift, Sütterlin
Wochentage im Kopf
Transkription
Wurzel Herleitung
Wurzel
Wortwoertlich
Deutsche Verbformen generieren
Verbformen generieren, konjugieren