Polynomdivision für Casio Rechner
|
|
|
auf dieser seite stelle ich ein programm vor, welches eine polynomdivision beliebigen grades auflöst. den zugrunde liegenden algorithmus habe ich (mühsam) hergeleitet und schließlich auf einem "casio cfx9850g" implementiert. er lässt sich aber ohne weiteres in anderen programmiersprachen umsetzen.
Mathematisches... |
|
an dieser stelle erläutere ich kurz die formeln, die durch das programm letztendlich abgebildet werden. vielleicht kennt jemand einen anderen lösungsansatz als den hier dargestellten - ich finde aber nach etwas einarbeitung kann ihn jeder verstehen. ich habe aus diesem grund auch ein beispiel mit abgebildet.
der ausgangspunkt für die findung der formeln war eine allgemeine form des aufzulösenden bruchs. mit diesem habe ich dann eine polynomdivision durchgeführt wobei sich die folgenden 4 formeln ergeben haben:
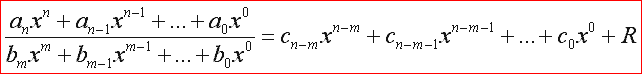
Abb 1: allgemeine form des bruches = ergebnisvektor + rest "R"
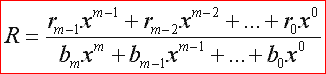
Abb 2: R = restvektor
abbildung 1 zeigt die allgemeine form eines bruches, der durch eine polynomdivision vereinfacht werden soll. im zähler sind dabei die koeffizienten a und im nenner die koeffizienten b durch eine konkrete aufgabe vorgegeben. der ergebnisvektor enthält als auszurechnende elemente die koeffizienten c. der restvektor in abbildung 2 enthält dann die ebenfalls auszurechnenden koeffizienten r.
für beide formeln lassen sich folgende (in abbildung 3 dargestellte) bedingungen festlegen:
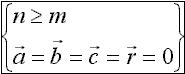
Abb 3: bedingungen der formeln
diese besagen zum einem, dass der größte exponent im zähler (n) größer oder zumindest gleich dem größten exponent im nenner (m) sein muss. zum anderen sollen die vektoren a, b, c und r gleich null gesetzt anzeigen, dass alle nicht verwendeten koeffizienten (z.B. a123 oder b-3) mit null vorbelegt sind. greift also die nachfolgende berechnung auf nicht definierte koeffizienten zu, ist hierfür einfach null einzusetzen.
die formel aus abbildung 4 zeigt die berechnung der einzelnen koeffizienten c aus dem ergebnissvektor. hierbei wird mit cn-m begonnen um sukzessive alle koeffizienten bis hin zu c0 zu berechnen. die reihenfolge ist zwingend einzuhalten, da schon berechnete c's in darauffolgenden berechnungen benötigt werden!
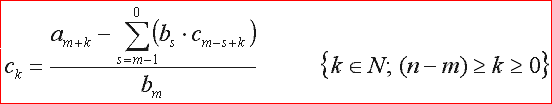
Abb 4: koeffizienten c im ergebnisvektor
das gleiche gilt für die koeffizienten des restvektors. hier wird nach der formel aus abbildung 5 mit rm-1 begonnen und auf r0 hingearbeitet. da zur berechnung von r die werte von c notwendig sind, kann diese zwingenderweise auch nur nach der berechnung aller notwendigen c-werte stattfinden.
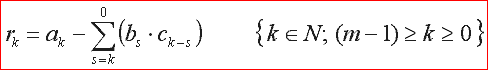
Abb 5: koeffizienten r im restvektor
Beispiel... |
|
mit dem folgendem beispiel sollen die formeln von eben etwas ins praktische licht gerückt werden. in abbildung 6 ist eine beispielaufgabe mit ergebnis und rest dargestellt. abbildung 7 zeigt dann die werte der durch die aufgabe vorgegebenen koeffizienten (a und b) und die berechneten koeffizienten (c und r) an.
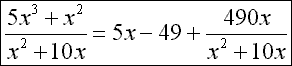
Abb 6: beispielaufgabe mit lösung (ergebnis und rest)
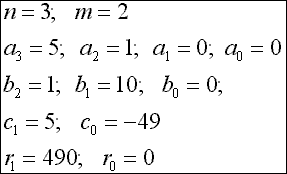
Abb 7: koeffizienten a, b, c und r zur aufgabe aus abbildung 6
um das prinzip der formeln zu verstehen, sollte man diese aufgabe einmal händisch nach ihnen berechnen.
Programm... |
|
hier folgt der quelltext des programmes "polynom". das doppelkreuz "#" soll den ausgabebefehl (kleines dreieck unten rechts) und der schräger "/"das bruchsymbol (kleine ecke unten rechts) darstellen.
das programm kann auch hier als textdatei  polynom.txt heruntergeladen werden.
polynom.txt heruntergeladen werden.
programm "polynom" |
|
|
als beispiel soll wieder die aufgabe aus abbildung 6 dienen. hierzu stelle ich nun den dialog zwischen programm und demjenigen der die aufgabe lösen will dar. es sei noch einmal erwähnt, dass die koeffizienten a und b aus abbildung 7 als eingabe des programmes dienen und die koeffizienten c und r vom programm ausgegeben werden. (benutzereingaben sind fett hervorgehoben)
programmdialog | zugehörige koeffizienten |
|
Gr.Exp.Zahler? 3 Gr.Exp.Nenner? 2 A: 5 A: 1 A: 0 A: 0 B: 1 B: 10 B: 0 Gr.Exp.Ergebnis
1 -Disp-
Ergebnis:
5 -Disp- -49 -Disp-
Gr.Exp.Rest
1 -Disp-
Rest:
490
-Disp- 0 -Disp- |
=n =m =a3 =a2 =a1 =a0 =b2 =b1 =b0 =c1 =c0 =r1 =r0 |
wie man sieht, muss dem programm gesagt werden, was der größte exponent im zähler und nenner ist. daraufhin ist das programm in der lage die einzelnen koeffizienten (erst a dann b) von links nach rechts (vom größten zum kleinsten exponent) abzufragen.
wurde diese eingabe gemacht, gibt das programm die lösung aus. und das wieder zunächst mit der angabe der größten exponenten und anschließend von links nach rechts (vom größten zum kleinsten exponent) die einzelnen koeffizienten des ergebnisses und des restes (c und r).