Römische Zahlen
Römische Zahlen bzw. römische Ziffern findet man heute vor allem in Form von Jahreszahlen an historischen Bauwerken oder in Dokumenten,
da Jahreszahlen oft noch Jahrhunderte nach Untergang des Römischen Imperiums derart angegeben wurden.
Weiterhin werden römische Zahlen auch in Chronogrammen, zur Unterscheidung von Herrschern einer Dynastie
mit demselben Vornamen, zur Numerierung von Gliederungsebenen in Büchern und Dokumenten oder auch zur
Unterhaltung bei den sogenannten "Streichholz-Rätseln" verwendet.
Programm: Umrechner in und von römischen Zahlen
Umrechner für römische Zahlen
Nutzen Sie dieses Programm zum Umwandeln von dezimalen in römische Zahlen und umgekehrt.
Eventuelle Fehler oder Warnungen werden im Feld Bemerkungen angezeigt.
Tragen Sie die roemische Zahl im blauen oder grünen Feld ein und klicken sie auf den entsprechenden
Pfeil. Die dezimal umgerechnete Zahl wird dann im oberen Feld angezeigt. Um eine dezimale Zahl in eine
römische umzuwandeln, tragen Sie sie ins obere Feld ein und drücken den braunen Pfeil.
| Grundzeichen (GZ) |
Hilfszeichen (HZ) |
| Zeichen |
Wertigkeit |
Zeichen |
Wertigkeit |
| I |
1 |
V |
5 |
| X |
10 |
L |
50 |
| C |
100 |
D |
500 |
| M |
1000 |
|
|
Abbildung 1: Grund- und Hilfszeichen
Römische Zahlzeichen
Das römische Zahlensystem ist im Gegensatz zu unserem heutigen Stellenwertsystem ein
sogenanntes Additionssystem. Bei einem Stellenwertsystem ist die Wertigkeit einer Ziffer auch abhängig von deren
Stellung innerhalb der Zahl
(z.B. 3531 = Ziffer 3 hat einmal Wertigkeit 3000 und einmal 30). Dem entgegen hat jede Ziffer bzw. jedes Zeichen bei
einem Additionssystem, unabhängig vom Auftreten innerhalb des Zahlwortes, die gleiche Wertigkeit. Additionssystem bedeutet
weiterhin, dass sich der Wert des Zahlwortes aus der Addition der Wertigkeiten aller aufgeführten Zeichen ermittelt.
| Zeichen |
Wertigkeit |
Zeichen |
Wertigkeit |
 |
50 |
CI oder
oder 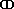 |
1.000 |
I oder D oder D |
500 |
CCI  oder
oder
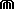 oder
oder
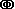 |
10.000 |
I  oder
oder 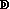 |
5.000 |
CCCI   oder
oder
 oder oder
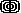 |
100.000 |
I   oder
oder 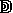 |
50.000 |
| ... |
... |
... |
... |
Abbildung 3: Zeichen höherer Wertigkeit
Abbildung 1 zeigt die Grund- und Hilfzeichen, die zur Darstellung verwendet werden. Die Wertigkeit der Grund- und Hilfszeichen wird
dabei addiert. Die Hilfszeichen bilden jedoch eine Ausnahme. Ihr Wert wird bei entsprechender Stellung im Zahlwort subtrahiert
(siehe unten "Subtraktive Kombination"). Dies wurde erst später zur Vereinfachung eingeführt und war ursprünglich nicht
Bestandteil dieses Zahlensystems.
| Zeichen |
Wertigkeit |
 |
Multiplikation mit 1.000
Bsp: 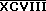 = 98.000 = 98.000 |
 |
Multiplikation mit 100.000
Bsp: 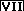 = 700.000 = 700.000 |
Abbildung 2: Multiplikatoren
Die Zahl 0 konnte nicht dargestellt werden. In einem Additionssystem ist die jedoch auch nicht
notwendig. Zur Angabe von Mengen wurde in diesem Fall einfach das Wort "Null", "Kein", "Nichts" usw. verwendet.
Zur Darstellung von größeren Zahlen ist die gebräuchlichste Variante der Einsatz von Multiplikatoren. Quergestrichene Zahlen
entsprechen dem Wert des Zahlworts multipliziert mit 1.000, eingerahmte Zahlwörter einer Multiplikation mit 100.000.
Abbildung 2 stellt diese Varianten dar.
Weiterhin existieren zusätzliche Zeichen mit höheren Wertigkeiten.In der Regel handelt es sich
um zusammengesetzte Zeichen, die auch kombiniert dargestellt werden können. Zumeist findet ein
gespiegeltes "C" Anwendung. In Verbindung mit einem "I" wird es auch als "D" dargestellt. Abbildung 3 zeigt
Zahlzeichen bis 100.000.
Beispiele römischer Zahlwörter
In Tabelle 1 sind Beispiele römischer Zahlen dargestellt.
| Dezimal |
Römisch |
Römisch |
|
Dezimal |
Römisch |
Römisch |
|
Dezimal |
Römisch |
Römisch |
| 1 |
I |
I |
|
11 |
XI |
XI |
|
70 |
LXX |
LXX |
| 2 |
II |
II |
|
12 |
XII |
XII |
|
80 |
LXXX |
LXXX |
| 3 |
III |
III |
|
13 |
XIII |
XIII |
|
90 |
XC |
XC |
| 4 |
IV |
IV |
|
... |
... |
... |
|
98 |
XCVIII |
XCVIII |
| 5 |
V |
V |
|
19 |
XIX |
XIX |
|
99 |
IC |
XCIX |
| 6 |
VI |
VI |
|
20 |
XX |
XX |
|
100 |
C |
C |
| 7 |
VII |
VII |
|
30 |
XXX |
XXX |
|
110 |
CX |
CX |
| 8 |
VIII |
VIII |
|
40 |
XL |
XL |
|
200 |
CC |
CC |
| 9 |
IX |
IX |
|
50 |
L |
L |
|
999 |
IM |
CMXCIX |
| 10 |
X |
X |
|
60 |
LX |
LX |
|
1000 |
M |
M |
Tabelle 1: Beispiele römischer Zahlwörter
Detaillierte Darstellungsregeln
Für das Lesen und Schreiben von römischen Zahlwörtern gelten die folgenden Regeln. Hierbei muss man
jedoch 2 verschiedene Varianten beachten. Zum einen die allgemeinen Regeln und zum anderen die hauptsächlich an
Schulen gelehrten Ergänzungen zu den Regeln.
| 1 |
Die Grundeinheit eines römischen Zahlwortes soll hier als "römisches Ziffernzeichen" RZ bezeichnet werden. Ein römisches Zahlwort besteht hernach aus einer Aneinanderreihung von RZ.
| |
Bsp: römisches Zahlwort = MMDIX besteht aus den RZ: "M", "M", "D", "IX"
|
|
| 2 |
Ein RZ ist entweder ein Grundzeichen GZ, ein Hilfszeichen HZ oder eine "subtraktive Kombination" SK (Definition SK siehe Regeln 7-9).
| |
Bsp: MMDIX besteht aus folgenden RZ: "M" = GZ, "M" = GZ, "D" = HZ, "IX" = SK
|
|
| 3 |
Jedes RZ besitzt eine definierte Wertigkeit. Für GZ und HZ ist die Wertigkeit in der obigen Tabelle angegeben. Für SK ist die Wertigkeit den Regeln 7-9 zu entnehmen.
|
Bsp: Wertigkeit von HZ "V" ist 5
Bsp: Wertigkeit von SK "IV" ist 4
|
|
| 4 |
In einem römischen Zahlwort sind die einzelnen RZ mit absteigender Wertigkeit von links nach rechts sortiert angeordnet.
| |
Bsp: MDCCXIII (M > D > C > X > I)
|
|
| 5 |
Der Wert eines römischen Zahlwortes bestimmt sich aus der Summe der Wertigkeiten der einzelnen RZ
| |
Bsp: MDVII = 1000 + 500 + 5 + 1 + 1 = 1507
|
|
| 6 |
Ein RZ aus dem selben GZ darf höchstens 3 mal und aus dem selben HZ sowie aus der selben SK darf höchstens einmal erscheinen. Eine Ausnahme bildet die Zahl 4 (= IIII) auf Zifferblättern von Uhren.
| |
Bsp: 66 ist nicht XXXXXXIIIIII sondern LXVI
|
|
| 7 |
Eine SK besteht aus 2 Zeichen, wobei ein GZ links von einem GZ oder HZ größerer Wertigkeit steht.
| |
Bsp: XD = GZ X steht vor HZ D; wichtig: D hat höhere Wertigkeit als X
|
Besondere Regel: (wird hauptsächlich an Schulen gelehrt)
I steht nur vor V und X
X steht nur vor L und C
C steht nur vor D und M
|
|
| 8 |
Die resultierende Wertigkeit einer SK ist die Differenz zwischen den Wertigkeiten der beiden enthaltenen GZ und/oder HZ.
| |
Bsp: XD = 490; IC = 99; IV = 4
|
|
| 9 |
Rechts neben einer SK dürfen nur RZ folgen, welche GZ und/oder HZ enthalten, die eine niedere Wertigkeit besitzen, als der linke Bestandteil der besagten SK.
| |
Bsp: falsch: XCIX = 99; richtig: IC = 99
| |
Bei der Beachtung der besonderen Regel 7, gilt diese Regel 9 nicht.
| |
Bsp: richtig: XCIX = 99; falsch nach regel 7: IC = 99
|
|
| 10 |
Die zusätzlichen Zeichen ZZ können auch mit GZ und/oder HZ kombiniert werden. |
Bsp: CI I I XCVIII = 1598
XCVIII = 1598
|
|
Weiterführende Seiten
Umrechnung von (ganzzahligen) Dezimalzahlen in Römische Zahlen

 oder
oder 
 oder D
oder D
 oder
oder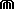 oder
oder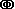

 oder
oder 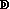


 oder
oder oder
oder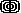


 oder
oder 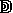

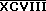 = 98.000
= 98.000
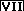 = 700.000
= 700.000